旅行者一号探测器在浩瀚的宇宙中享受星际之旅,飞行的几十年来它不仅看过许多景色,而且还用照片的形式记录下来了,人类喜出望外的同时发现旅行者一号发回神秘照片竟然透露着恐怖,这些照片有何恐怖之处呢?下面小编就和大家一起了解下吧!...
发布时间:2024-09-21 06:02:48
方程和数字一样,不是总能被分解成更简单的元素。研究人员现在证明:随着方程增大,“质数”方程将无处不在。质数之所以深受喜爱,是因为它成为无数流行报道的焦点,也是数学中最著名开放性问题的掌上明珠。但有一个同样是基础性的数学问题却很少受到关注:质数方程。质数方程式中,特别是多项式方程,不能被其他任何方程式分解。和质数一样,它们也是数学研究领域的核心。对于许多特定问题,如果你能理解一些关于质数方程的知识,你会发现你已经回答了实际要解决的问题。

特拉维夫大学(Tel Aviv University)的里尔•巴里-索罗克(Lior ry- soroker)表示:当我们遇到问题时,将它总结归纳为质数方面的知识,多项式也是如此。质数方程的最基本知识与质数类似:出现频率,在过去的一年中,数学家们在这个问题上取得了重大进步。十月底发表的一篇论文中,剑桥大学的艾曼纽·布勒亚尔(Emmanuel Breuillard)和彼得·瓦居(Peter Varju)证明:几乎所有特定类型的方程都是质数。这意味着质数方程与罕见的质数不同,质数方程更为丰富。新论文解决了已有25年历史的数学猜想,从在线加密到随机数学,其意义无处不在。
1、失败的途径越多
数学中的许多问题可以归纳为多项式方程,这些方程——就像y = 2 x−3 和y = x2 + 5 + 6,系数在变量之前,变量逐渐上升到幂。在许多方面,方程式表现得与普通的数字别无二致:也可以进行加、减、乘、除运算。人们很自然地会问,哪些方程能够表示为两个较小方程的乘积。当一个方程不能被分解成两个更小的方程时,数学家们就说它不可约。现在,数学家们想知道不可约多项式方程多久能出现一次。试图在所有可能多项式(具有任意数量的变量、升到任意幂、具有任意系数的方程)中,陈述出不可约多项式的频率极其困难。因此数学家们通过限制指数或将系数限制在小范围内来解决这个问题。

某些多项式方程能分解成几个小部分。图片:Hannah Li for Quanta Magazine
2017年10月以色列Weizmann科学研究所数学家巴里-索洛克(barry - soroker)和盖迪·科兹(Gady Kozma)证明了几乎所有系数范围内有限多项式都不可约。不久布勒亚尔和瓦居解决了一个与之稍有不同的问题。他们考虑了任意长度、任意指数、任意系数的多项式(唯一的限制是可能系数的数量有限)。布勒亚尔和瓦居的方法能够解决更简单的问题。1993年现任明尼苏达大学( University of Minnesota)的数学家安德鲁·奥德利兹科( Andrew Odlyzko)和现任麻省理工学院的比昂·庞宁(Bjorn Poonen)推测:当考虑系数必须为是0或1的复杂多项式时,可分解方程就变得非常罕见、
奥德利兹科和庞宁猜想,通过限制多项式的系数是为了在压倒性问题中站稳脚跟。巴里-索罗克说:如果你想学习一些知识,证明很多观点,那你最好从简单的事情开始。他们的猜想也是基于基本算术,质数在前10个数字中很常见,但随着数字增多,质数开始变得越来越稀有。要成为质数,一个数字需要避免被比它小的整数整除(除了数字1)。为了使多项式能够进行因式分解,它的系数之间必须保持正确的关系。多项式y = x2 + 5x+ 6可以分解为(x + 3)×(x + 2),只是碰巧因为2和3两个数字相乘等于6,相加等于5。随着系数数量的增加,找到满足所有系数的因子的可能性越来越小。奥德利兹科说“多项式要可约,系数之间就必须保持特殊的关系,对于一个高次多项式来说,所要满足的条件就更多。
2、随机游动
布勒亚尔和瓦居并没有开始研究多项式不可约性,相反他们开始研究随机游走数学。在随机漫步中,想象你站在一个钟面上,时钟每隔一段时间就会标记出数字1到11。你从1对应的点开始抛硬币,如果硬币反面朝上,就将你所处位置的数字与事先选择的其他数字相乘,然后前进到圆上相应的点。在时钟或“模块化”数字系统中,如果输出的数字大于11,你就会一直不停地前行,直到达到所需的空格数为止。如果硬币正面朝上,在乘以所选数字的基础上加一,然后前进到相应位置。鉴于这些条件,布勒亚尔和瓦居想了解两件事:参观圆周上的每个点需要多长时间,参观完所有点需要多长时间?
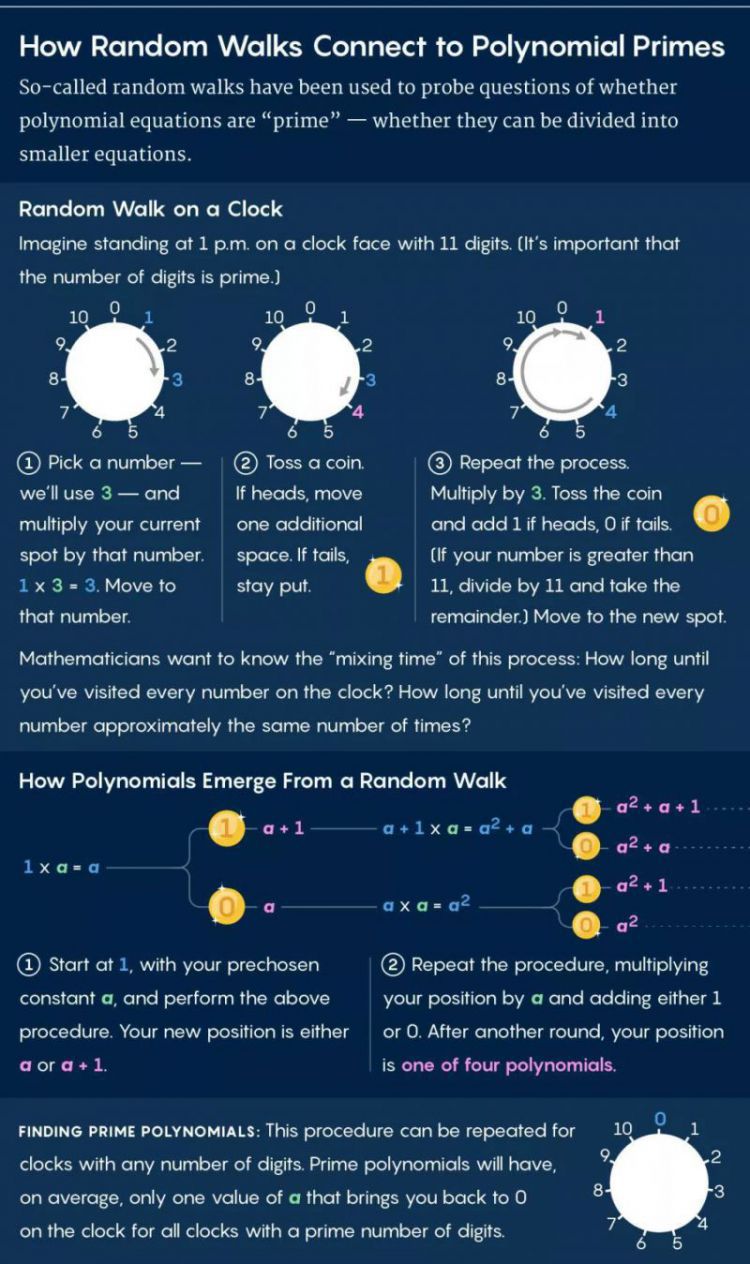
图片:Lucy Reading-Ikkanda/Quanta Magazine
数学家们把这些问题称为“混合问题”,它们与多项式不可约性相关。布勒亚尔和瓦居认识到,随机游动的路径可以分别用系数为0和1的多项式方程来描述。随机游动的“混合时间”与描述该随机游动的大多数多项式是否不可约密切相关。瓦居说:如果我们知道这些多项式是否不可约,就能对需要理解的问题做出一些解释。为了测试多项式的不可约性,布勒亚尔和瓦居采用了20世纪80年代开发的将不可约性与数论联系起来的技术。他们想知道一个给定多项式在给定的模数系统中有多少解。以前的工作已经表明,多项式的解数反映了因子的数量。如果它在模数系统中平均有三个解,它就有三个因数。如果多项式只有一个因子,这意味着它不可约。

布勒亚尔和瓦居将这种方法应用于基于质数的模数系统中,结论显示:当考虑越来越大的多项式(系数为0或1)时,多项式不可约的比例越来越接近100%。证明结果还取决于另一个猜想的真实性:黎曼假设。黎曼假设是数学中最重要、最令人畏惧的未解之谜。但黎曼假设被广泛接受,这在一定程度上支持了布勒亚尔和瓦居的工作。他们的研究结果具有广泛意义,在实践层面上,这对于在线加密来说是一个好消息,因为可分解多项式可能破坏常用的数字加密方式。更重要的是,这朝着理解方程本质迈出了一大步。方程在生活和数学中比比皆是,但数学家很难从整体上对它们加以描述。以前对多项式不可约的估计要弱得多,现在这些家伙说实际上它们都不可约。
博科园-科学科普|参考期刊文献:《arXiv》
文:Kevin Hartnett/Quanta magazine/Quanta Newsletter
Cite:arXiv:1810.13360
博科园-传递宇宙科学之美

钱姓排于百家姓中的第二位,虽然起源和来历并不多,但是钱姓人却分布广泛,成为了中国姓氏中的第二大姓。钱姓的主要来源就是彭祖的儿子篯孚,彭祖的真名叫做篯铿,是因为被尧封于大彭而得姓-彭,而他的儿子篯孚因为掌管着钱财,任职钱府上士,所以便为“钱”姓,所以彭钱是一家。...
发布时间:2024-09-20 20:03:27

胡服最早是由春秋战国时的赵武灵王-赵雍引入中原的,因为当时赵国的地形和地理位置都非常不好,常年深受战争威胁,加上赵武灵王继位之后,时局不稳,周边国家都想要攻打赵国,所以赵武灵王便下令让全员都推行胡服,并且学习骑射,相较于宽大的汉服更加便于行动。...
发布时间:2024-09-20 19:05:44

赛艇运动起源于英国的泰晤士河上,当时还是17世纪,英国泰晤士河上的船工在工作之余经常会举办一些赛船,久而久之就形成了一种习俗,在1715年的时候,为了庆祝英王的卫冕,所以第一次正式举办了赛艇比赛,最终在1775年发展为一个正式的运动项目,并且成立了相应的运动俱乐部。...
发布时间:2024-09-20 18:04:28

人们之所以不愿意或者不敢以“宸”为名,主要是因为在古时候“宸”有着“深邃的房屋”的意思,也就是专指皇帝的居住场所,象征着无上的权力,所以“宸”字自然也就成为了禁忌,不过现代人大多是害怕这个字的气势,普通人的命格扛不住。...
发布时间:2024-09-20 17:00:53

商细蕊是电视剧《鬓边不是海棠红》中的京剧名旦,很多人都为他和海归商人程凤台的知己故事而动容,但遗憾的是在历史长河中并没有商细蕊真正的原型,只能说他可能是作者根据历史上著名的京剧名旦构建的一个角色,因为他和梅兰芳、程砚秋、尚小云以及徐碧云等四人的经历和性格都有着极为相似之处。...
发布时间:2024-09-20 16:05:01

在中华上下五千年的历史长河中,除了王朝更替的政治生活与文化生活,还有一些美貌的女子点缀着历史的绘卷,那么在悠悠岁月中有哪些著名的美女呢?下面小编就来为大家盘点一下吧!...
发布时间:2024-09-20 15:04:04

谈及古代帝王,最让人津津乐道的当属那后宫佳丽三千,不过也不是所有的帝王都有那么充实的后宫,比如历史上有一位皇帝就只有一位妻子,是不是让人有点不敢相信,下面小编就带大家一起了解下吧!...
发布时间:2024-09-20 14:01:05

自古无情帝王家,说到帝王的爱情多是奢望,很多帝王后宫的妃子换了一个又一个,几乎都是薄情寡义的,但是漫长的历史长河中也有例外,有的皇帝便与众不同,特别的长情,下面小编来为大家介绍一下历史上最长情的皇帝吧!...
发布时间:2024-09-20 13:03:24

可以说人的成长伴随着无数的武侠剧,尤其是电视剧中的那些绝世高手更是让人影响深刻,有不少人小时候都幻想过可以武功盖世,一统江湖,那么有人知道武侠剧中有哪些绝世高手吗?下面小编为大家盘点一下吧!...
发布时间:2024-09-20 12:02:19

古装电视剧中有许多的美丽的女子,她们身着美丽的衣裳,一举一动摇曳生姿,美得让人挪不开双眼,可以说是一场视觉盛宴,下面就让小编为大家盘点一下那些古装美女吧!...
发布时间:2024-09-20 11:09:01

近年清朝古装剧收视率暴涨,这些电视剧不仅剧情引人入胜,身着清装的美人也同样吸引了不少目光,有着让人过目不忘的美貌,那么清朝古装剧中有哪些美人呢?下面小编就来为大家盘点一下吧!...
发布时间:2024-09-20 11:02:08

养龟市场上经常可以看到小青龟,这种乌龟乖巧可爱以及性情温顺,所以很多人都会选择小青龟来饲养,不过一直都是见到小青龟都比较小,这不禁令人好奇这种乌龟能长多大?下面小编就带大家一起了解一下小青龟吧!...
发布时间:2024-09-20 10:01:47